There’s both a mathematical explanation and an explanation based on the nature of reality.
First, the mathematical explanation: Let’s take the example of the Double Slit Experiment. A laser shoots photons one-at-a-time through the two slits of a
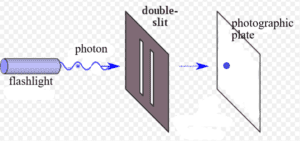
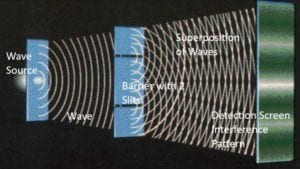
The mathematical expressions for the wave amplitudes often include complex numbers (numbers that include the square root of negative 1). We cannot visualize such a number because what number multiplied times itself equals negative 1? There is no such number. We label this non-number as i and just don’t try to imagine what amount i really represents. Even though i does not describe anything that we’re familiar with in the physical universe, both mathematicians and physicists have found it useful to work equations which include i, that is, complex numbers.
But returning to the wave function in the Copenhagen Interpretation. Max Born (1882-1970) was the quantum physicist who first realized that the amplitude of the quantum wave predicts the probability of detecting a particle in a particular position. But this creates a problem. What if the amplitude includes a complex number?
A probability cannot be expressed using complex numbers. Probabilities are expressed as positive numbers ranging from 0% to 100%. That is, we can say that there’s a 50% chance when tossing a coin of getting heads. Or a 0% chance that every moment of the day will be fun. And a 100% chance that a human being will eventually die. But to say that the chances of an event are the square root of negative 1 makes no sense.
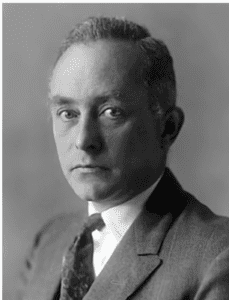
This calculation is the Born Rule. Experimental results show that the Born Rule is accurate in calculating quantum behavior. So, not only does the rule cancel out the troublesome complex numbers, it accords with empirical results. The Born Rule is an integral part of the Copenhagen Interpretation.
However, the Born Rule does not explain what is happening in the physical universe that requires that we multiply the wave amplitude by its complex conjugate. Nor does any other part of the Copenhagen Interpretation provide such an explanation. The Transactional Interpretation does. While it would be too lengthy to fully explain this interpretation here, an example gives a taste:
Let’s say take a look again at the Double Slit Experiment with a laser emitting a single photon towards a photographic plate. Until it arrives at the photographic plate, it’s a quantum wave that physicists can calculate a wave function for. The wave function identifies the possible positions where the quantum wave could deposit its energy on the photographic plate. So far, this is like the Copenhagen Interpretation. But the Transactional Interpretation adds something new. It says that if the photon is to land on the photographic plate, an electron in the plate must take action to absorb it. Electrons in the plate must send out their own waves. When the emitting wave and the receiving wave interact, the photon transfers energy to the electron, and takes its place in physical reality at a position on the plate.
The wave function of the absorbing electron in the plate has an amplitude that fits well with the amplitude of the photon: it’s the complex conjugate of the photon’s amplitude.
But why multiply the two amplitudes? This is how we find the probability of two events occurring, in this case both the photon heading towards a particular position on the plate and an electron in that position absorbing it. When we calculate the probability of any two events, we multiply the two probabilities. For example, the chances of a baby being born a girl with brown eyes is: 1) the probability of being a girl (about 48%) times (2) the probability any baby having brown eyes (about 80%). We multiply 48% times 80% and get 38%. There’s a 38% chance that a baby born anywhere in the world will be a girl with brown eyes.
The emitting wave and the absorbing wave have to interact if the photon is to land in any particular position. We multiply the probability of the photon landing in a particular position (the complex number describing the amplitude) times the amplitude of the receiving wave at that position on the plate (the complex conjugate).
The Transactional Interpretation is based on Absorber Theory developed by Richard Feynman and John Wheeler in the late 1930’s. It was fully developed as an interpretation of quantum mechanics by John Cramer in the 1980’s and further developed by Ruth E. Kastner. Kastner has written technical papers on the Transactional Interpretation and also a book for laypeople, Understanding Our Unseen Reality. I highly recommend the book because it provides a coherent and understandable explanation of the physical meaning quantum mechanics.
