« Back to Glossary Index

The Heisenberg Uncertainty Principle (HUP) is also called the “Indeterminacy Principle” or simply, the “Uncertainty Principle.” It says that some of the properties of atoms and the components of atoms have an inherent fuzziness. For example, it is not possible to discover with precision both the momentum and the position of a quantum particle simultaneously. Indeed, the particles do not have precisely defined momentum and position at the same time. To the degree the position of a particle is precise, to that degree the momentum is imprecise. And vice versa.

Further, if the momentum is measured and then, the position is measured, the original measurement of momentum is no longer accurate. This is because the particle will now have a new momentum. And vice versa: If the position is measured and then, momentum is measured, the position measurement will have been invalidated and rendered inaccurate due to the position having changed. In summary, we will get different measurements if we measure the momentum first than if we measure the position first.

The HUP applies to each individual particle.

The Nobel Laureate, Frank Wilczek, puts it this way, “According to the original uncertainty principle, to pin down the position accurately we must live with a large uncertainty in momentum.  (Note: Werner Heisenberg in developing his principle originally addressed position and momentum; later his principle was expanded to include properties additional to position and momentum.) In another description of the principle, Wilczek writes, “According to the Heisenberg uncertainty principle, in order to have accurate knowledge of the position of a particle, you must let that particle have a wide spread in momentum. In particular, you must allow that the particle may have large momentum.” (italics per original)

Jim Al-Khalili, a leading quantum physicist, gives an example of the uncertainty principle at work. He explains why the negatively-charged electron doesn’t fall into the positively-charged nucleus. “Heisenberg’s uncertainty principle tells us that trapping a quantum particle [electron] within the tiny confines of a nucleus would imply knowing its position to high accuracy. This corresponds to its momentum being too erratic for the attractive force of the protons to keep it there for long. Quantum particles [electrons] simply could not be imprisoned inside the nuclei.”⁴

While Al-Khalili uses the word “knowing” in his explanation, he is explaining more than our lack of exact knowledge. He is explaining why the electron does not, in fact, limit itself in position to a small space like the nucleus. And why the electron, instead, occupies a space around the nucleus that is analogous to a cathedral when viewed by a grain of salt. If the electron were pinned down to the tiny space of the nucleus rather than the cathedral, its momentum would vary so wildly, due to the HUP, that the positive electrical attraction could not hold it. The quantum particle would fly out of the atom. The HUP is a law of nature which makes atoms possible. The HUP is not just about our knowledge of atoms. ⁵

Example of Heisenberg’s Uncertainty Principle

Let’s consider a laser that shoots its beam through a single slit (see image to left). Experiments show that if we narrow the slit, at first the light that lands on the screen also narrows. We are narrowing the width of the beam at the slit, which results in narrowing the width of the light received on the screen.

The beam is composed of photons. So, when we are narrowing down the slit, we are narrowing down the possible positions of the photons in the slit. We are making the positions of the photons more precise.

If we continue to squeeze the slit down to a narrower and narrower width, the positions of the photons at the slit are becoming more localized, more precise. But if we continue to squeeze the width of the slit, suddenly the width of the light on the screen broadens out. This broadening is illustrated in the accompanying image below. The image is a photo of actual experimental results.

The broadening of the light on the screen is due to changes in the momentum of the photons as they pass through the narrowed slit. Momentum is the amount of energy or mass hurtling in a certain direction at a certain speed. Suddenly, at the slit, the photons abandon a single direction and start traveling at a wider variety of angles along the horizontal axis towards the screen. Their directions are more varied which means that their momenta are more varied, that is, less precisely defined. It should be noted that if this experiment were done with single photon, the result would be the same: The light arriving on the screen would widen out. Its momentum would become fuzzy.

 

 

 

 

 

 

What has happened to our knowledge of the photons? We have more definite information as to their positions as they travel through the slit. We’ve narrowed down their position. But, what about their momenta? The screen shows us that their momenta now cover a wider range than before. We are less certain of the momenta of the photons because we are less certain of the angle of their trajectory towards the screen. But it is not just our knowledge that has become less precise; the actual momenta are less precise, more spread out. This is the Heisenberg Uncertainty Principle at work.

Pairs of Properties to which the Heisenberg Uncertainty Principle Applies

The original statement of the HUP, as formulated by Werner Heisenberg in 1927, regarded position and momentum. The HUP has since been discovered to apply to other pairs of properties. The most often mentioned is the energy level of a particle and the time during which the energy level applies.

This has implications for the mass of particles. The energy of a particle is convertible to its mass ⁶ due to Einstein’s equation E = mc² (where E = energy; m = mass; and c² = the speed of light squared). Very short-lived particles have precise “time durations,” that is, lifespans. Their lifespans are precise due to their brevity. Such lifespans leave very little wiggle room for variability. This means that, due to the HUP, their energy levels are difficult to pin down with measurements. When physicists measure the energy released upon the decay of very short-lived particles (or measure their mass), the results can differ upon different measurements. Their energy can range relatively widely.

The HUP applies, as well, to direction of spin: To the extent the up and down components of particle spin are precise, the left and right components of spin are imprecise. Other pairs are listed here.

Complementary Properties, Conjugate Pairs

Pairs of properties to which the HUP applies are called “complementary.” They are also called “conjugate pairs.”

Not all properties of quantum particles are subject to the HUP.

Not all properties of quantum particles are subject to the Heisenberg Uncertainty Principle. For example, the charge of a particle can be identified precisely. It’s “baked in.” All quantum particles have a charge of negative one. They’re born that way.

Heisenberg Uncertainty Principle is not due to clumsiness in measuring.

We might think that the fuzziness of certain pairs of properties is due to our inability to measure accurately. Or it might be due to clumsiness in conducting the experiment. These explanations are sometimes put forward by instructors and books.

Yes, measuring tiny particles like quantum particles is problematic. And it’s true that bouncing a photon off a quantum particle in order to observe it would change its momentum. But this is not the basic source of the uncertainty principle. The basic source lies within Schrodinger’s wave equation. It’s in the math itself.

Jim Al-Khalili, a noted quantum physicist, explains, “…[O]ne can never know at the same time the precise location and velocity of a quantum particle (or any other quantum entity). This is not, as many books might tell you, as a result of the experimenter giving the quantum particle an unavoidable random kick through the act of locating its position, and hence changing its speed and direction. Rather it is a consequence of the nature of the wavefunctions that describe the quantum particle’s possible location and state of motion even before we look.” ⁷

Heisenberg Uncertainty Principle, Mathematically

If you are not interested in the math of HUP, you can skip this section and, without losing the thread, go on to the next.

The Heisenberg Uncertainty Principle can be expressed as a simple mathematical equation.

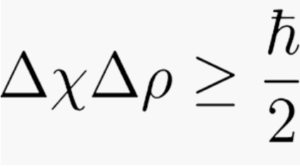Δ is the Greek letter delta and, here, means error in measurement or uncertainty. That is, Δ is the spread of values that you would get if you took a large number of measurements of the position of the particle. Technically, it’s the standard deviation of the square of the amplitude of the wave function.

x means the value of the position

p means the value of the momentum

≥ means greater or equal to

h is Planck’s Constant, an extremely tiny number

h-bar (line through the h) is a version of Planck’s Constant, ⁸ an incredibly tiny number. The symbol h–bar means h divided by 2 π.

p is pi, a constant that can be rounded to 3.14.

Limitation on HUP for Position and Momentum 

The HUP applies to position and momentum only on the same axis. In the example above of the photon traveling through the slit, the position of the photon is narrowed in regard to the x-axis (horizontally narrowed). This increases the fuzziness of its momenta in regard to the x-axis (horizontally). Were the slit narrowed in regard to the y-axis (vertically narrowed), then the photon, when hitting the detection screen, would spread out vertically rather than horizontally.

This means that it’s possible to obtain precise measurements of both position and momentum so long as each is measured in regard to a different axis.