« Back to Glossary Index

(Also called “observation”). Measurement is of considerable consequence in the quantum world. At least in some interpretations, through the act of measurement, the quantum particle transforms from a wave to a particle. Just as puzzling, the wave that is involved does not seem to fit our ordinary understanding of a physical wave. That’s measurement in a nutshell. If you want a step-by-step explanation, read on.

Measurement Defined

In quantum mechanics, when physicists measure a property of a quantum particle, they are really saying that they detect one of its properties. For example, let’s take the measurement of a photon in the famous Double Slit Experiment.

The description of this experiment could take a number of forms depending upon the specific interpretation of quantum mechanics. I will describe it in the terms of the original interpretation of quantum mechanics, the Copenhagen Interpretation.

Double Slit Experiment per the Copenhagen Interpretation

We hold an extremely dim laser light in front of a photographic plate. The laser is so dim that it emits only one photon at a time. A photon is the smallest bit of light possible. While scientists have found that a frog can detect a light as tiny as one photon, humans require several photons to become conscious of light.

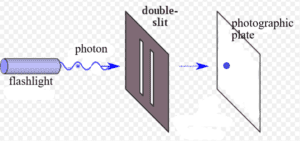
Getting back to the Double Slit Experiment, the laser shoots a photon that exposes the photographic plate in one spot and makes a dark dot. Once the photon hits the plate, we know the position of the photon—it’s a certain distance from each edge of the plate. So, we have detected it and, specifically, we have detected its position. Quantum physicists would say that we have “measured” its position.

This might seem just like measuring anything in our everyday world—for example, measuring the position of a bacterium. A biologist uses a microscope to detect the position of a living bacterium in a living human cell on a slide. She measures the distance of the bacterium from each edge of the cell. Here’s the difference: prior to the biologist measuring the position of the bacterium, the bacterium was happily swimming about the cell. After the measurement, same thing: happily swimming bacterium.

What was the photon doing before the measurement, before it hit the photographic plate? The Copenhagen Interpretation is inscrutable on this point. Here, in essence, is what it says: Prior to hitting the plate, the photon was in all possible positions in the photographic plate and maybe elsewhere as well. This condition of being in many possible positions is called a “superposition.” A superposition is a state in which we never observe a physical object. Have you ever seen an object occupy many positions at the same time? Neither have I. Nevertheless, prior to measurement, physicists say that the photon is in every possible position that the laser could have shot it to.

The condition of being in a superposition is also called a “quantum state.” It is the condition in which the weird behavior of quantum mechanics occurs.

Superpositions are mathematical rather than physical.  

How do physicists know that quantum particles are in a superposition prior to detection? After all, the physicists haven’t detected anything yet. Equations tell them this. Schrodinger’s Equation, a key equation of quantum mechanics, can be used to calculate the position of quantum particles. (It can also be used to calculate other properties of quantum particles, like momentum.) Schrodinger’s Equation is a special type of equation which has as its solution, not a number, but yet another equation called a “wave function.”

If you understand the wave function, you will understand why measurement is such a key but odd aspect of quantum mechanics. In the explanation of the wave function, you won’t have to deal with complicated quantum mechanical equations. But it will take patience and a number of steps.

Wave Function Explained

The word “function” in “wave function” simply means a particular type of equation. If you’ve studied algebra, functions are old hat. For example, here is the function y = 2x. We say that y is a function of x.

The wave function is an equation that has a form that physicists are very familiar with, the form that might describe a water wave or a sound wave. So, it’s called a “wave function.” It’s in the class of equations that describes waves.

In the accompanying drawing, the red grid is supposed to be the graph ofa wave function—notice that  it includes a hump, that is, a three-dimensional wave. The green film represents the photographic plate. The orange dot is the position where the particle has been detected on the photographic plate. The green film is supposed to be showing a photon landing as a dot, not as a blob with the rest smeared out around it—as might be suggested by the shape of the wave in the red grid. While the wave function (red grid) describes a wave, that’s not what the photographic plate detects.

In the Double Slit Experiment and other quantum experiments, physicists find that the entirety of the particle is measured in a single position as a dot. We have no math that gets us from the wave function to the specific position that is detected in any particular run of the experiment. In any particular run, when the single photon shoots from the laser, the specific position in which it’s detected appears to be random. Nor does anything in the wave function suggest what might trigger the change from wave to dot.

Contrast this situation with calculations done in classical Newtonian physics about the behavior of everyday objects. For example, we could calculate whether a ball thrown against a window would bounce off it or would break it. We would need to know the mass, speed, and direction of the ball. We would also need to know the force required to break the glass. With these numbers, we could calculate where on the glass the ball would hit, the force it would exert, and, thus, whether the glass would break. No mystery.

In quantum mechanics, we don’t know of a calculation that describes the shift from wave to particle nor how to calculate where the particle will land. In fact, some interpretations of quantum mechanics (as described below in the section on the De Broglie-Bohm Interpretation) maintain that no such shift from wave to particle occurs. The puzzlement and debate regarding the shift from wave to particle is called the “Measurement Problem.”

The wave function describes collective runs of the experiment.

So, what is the evidence that the wave function calculates the behavior of the photon prior to detection? Physicists have found that it calculates the collective behavior of many runs of the experiment. If we repeat the experiment over and over, each time shooting just one photon at the photographic plate, the dots start to build up into a striped pattern. The accompanying photos show this gradual build-up. This is a sequence of photos of a detection screen starting with a and ending with e. These photos show the results of a Double Slit Experiment in which electrons rather than photons were used. But the principle is the same.

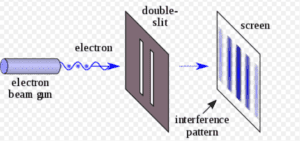
This striped pattern is highly recognizable to physicists. It’s called an “interference pattern.” It’s the signature pattern of two waves meeting. For example, physicists see it when two water waves meet or two sound waves meet. Particles don’t create this pattern; only waves do.

The Interference Pattern

The accompanying drawing shows how an interference pattern is created by water waves.  A single wave on the left approaches a barrier with two slits. The wave divides in two after passing through the slits. The crests and troughs of the two waves create the familiar criss-cross pattern of ripples that we see if we throw two pebbles into a pond. The two waves have “interfered” with each other, creating an interference pattern.

Here’s the punchline: the wave function in the Double Slit Experiment doesn’t calculate the position of the particle on any particular run of the experiment; rather, it calculates the photons collectively. Over time, the photons collectively create the pattern that results when two waves interact, an interference pattern. It’s able to do this because the wave function calculates the probabilities of where the photons will land on the photographic plate.

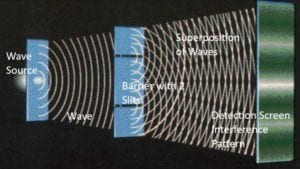
Returning to the drawing of the red grid and green film, the shape of the red-grid-wave reflects probabilities as to where the quantum particle might be detected. The wave is highest where the probabilities of detection are highest; the wave is lowest where the probabilities of detection are lowest. The wave function tells us about the probabilities of particle detection which, in turn, determines the shape of the interference pattern. The maximum exposures of the photographic plate (the darkest stripes) will occur where the photons have the highest probability of hitting the photographic plate.

Measurement and the Collapse of the Wave Function

Prior to detection, the photons appear to be waves: they form an interference pattern as waves do. But upon detection, the photons land as dots on the photographic plate, as a particle would. Some people describe this as traveling as a wave but landing as a particle. This is the famous quantum particle-wave duality. Measurement (detection on the photographic plate) is said to cause the “collapse of the wave function,” that is, the collapse from wave to particle.

What kind of wave is described by the wave function?

What kind of wave could create an interference pattern that builds up one particle at a time? What could it be made of? This was a puzzle to the physicists who founded quantum mechanics in the 1920’s and ‘30’s, and it remains a puzzle to this day.

The first stab made at understanding this wave was by the physicist who first related the wave function to the probabilities of particle detection, Max Born. In 1926, Born published the mathematical formulation of his discovery that the wave function calculates the probabilities of where particles will be detected, the “Born Rule.” This discovery was awarded a Nobel Prize in 1954.

Born said that the wave function is a “probability wave” and wrote:

“I personally like to regard a probability wave as a real thing, certainly as more than a tool for mathematical calculations. … how could we rely on probability predictions if we do not refer to something real and objective? (Max Born on Quantum Theory)”

In this view, the wave function, a math equation, is granted physical reality in the form of a wave of probability. But probability, of course, is also a mathematical concept and has no physical reality. This is a puzzling aspect of the Copenhagen Interpretation and is part of the “Measurement Problem.”

Bohmian Interpretation of the Wave Function

In the 1950’s, an alternative to the Copenhagen Interpretation, the De Broglie-Bohm Interpretation, was developed by the physicist, David Bohm. He built on

the work of one of the founders of quantum physics in the 1920’s, Louis De Broglie. The De Broglie-Bohm Interpretation relies upon the same mathematical equations as the Copenhagen Interpretation, though it creates an additional equation. It says that the wave function describes a real wave, called a “pilot wave” or “guiding wave.” In this view, measurement does not cause wave function collapse and the formation of a particle. Instead, the photon starts as a particle and ends as a particle.

But the particle is guided by an associated wave. The guiding wave splits in two at the two slits. As the two parts of the wave meet, they create an interference pattern. The photons which travel on these waves trace this interference pattern. The accompanying illustration of the surfers on a wave show this basic concept: objects being guided by a wave.

This explanation so appeals to common sense, that you might wonder why it isn’t universally accepted as the true interpretation of the Double Slit Experiment. However, the De Broglie-Bohm Interpretation has never been terribly popular among physicists. This is, at least in part, because the wave function describes a wave that really doesn’t fit well into the physical universe.

Apparent non-physical properties of the wave function:

• The wave function can include the imaginary number i, that is the square root of negative 1. But no number multiplied by itself equals negative 1. So, what physical thing could can be described by the square root of negative 1? As Dr. Ruth E. Kastner writes, “Anything observable in the world of appearance must be described by real numbers [not imaginary numbers]….”
• We know of no medium in which the guiding wave is traveling. A wave is nothing more than a vibration. What is vibrating? Some people say that quantum waves are unique in that they don’t require a medium. But these words only paper over this logical problem.
• If an interaction of two or more particles is being described, the wave function includes more than three spatial dimensions. As current understanding of the physical universe includes only three spatial dimensions, the wave, as described, doesn’t seem to fit into physical reality.

These properties of the wave function lead to the conclusion that it is describing something other than a physical wave. David Bohm proposed that the guiding wave is, in fact, not part of ordinary physical reality. He called it a “quantum potential.” He described it as a new force of nature and added an equation for it to the generally-accepted equations of quantum mechanics.

Many physicists don’t buy that a wave that isn’t part of physical reality could guide particles that they see land on their photographic plates. Others reject the guiding wave on the basis of Ockham’s Razor: quantum mechanics works fine without the equation which describes the guiding wave. For about a century, physicists have been able to accurately predict the results of experiments and to develop computer technologies with the quantum mechanical equations of the Copenhagen Interpretation. Why add another force of nature and its equation?

Interpretations of Quantum Mechanics and the Measurement Problem

Physicists agree on the workability of current quantum physics equations for predicting the behavior of quantum particles in experiments. However, they have developed over 10 interpretations of the physical meaning of these equations. These interpretations mostly differ in their explanations of wave-particle duality and the role of measurement.

The puzzling nature of what is actually happening when a quantum particle is measured is called the “Measurement Problem.” The Measurement Problem has two parts: 1) What triggers the wave to collapse down to a particle, what is the exact mechanism of collapse, and how can it be described mathematically? 2) What causes the particle to select a particular property, such as a particular position, rather than another from among the possible positions in the superposition? It should be noted that these statements of the Measurement Problem are phrased in the terms of the Copenhagen Interpretation. Several interpretations, like the De Broglie-Bohmian, maintain that measurement does not cause wave function collapse and that there is actually no such thing as wave function collapse.

Heisenberg Uncertainty Principle

Yet another oddity besets measurement in the quantum world. Physicists have found experimentally that the more precisely the position of the photon is measured, the less precisely its momentum can be measured and vice versa. This is called the “Heisenberg Uncertainty Principle.” In the 1920’s, Werner Heisenberg developed a mathematical equation describing the relationship between the precision of these two measurements. Since that time, physicists have found other pairs of properties that operate in a similar way—the measurement of one property impairs the ability to make an exact measurement of the other.

Summary

Measurement is the interface between the quantum world and the everyday world of tables and chairs. It is the point at which quantum wave-like behavior surfaces into our everyday world by creating a dot on a detection screen. The puzzles raised by measurement reflect differences between the laws that govern quantum particles and those that govern macroscopic objects like tables and chairs. The various interpretations of quantum mechanics, such as the Copenhagen Interpretation, the De Broglie-Bohm Interpretation, and the Many World Interpretation, provide different explanations for how the quantum world works and how it relates to the macroscopic world that we live in.