Many quantum physicists view quantum mechanics as differing from classical physics in a fundamental way—quantum mechanics is not deterministic. It is beset by “true randomness.” At the same time other physicists view quantum mechanics as deterministic. While there is considerable agreement among physicists on the mathematics and experimental results of quantum mechanics, there’s less agreement on how to interpret these, including in regard to determinism.
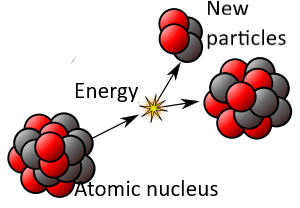
[Revision of the original image by Kjerish – Own work, CC BY-SA 4.0, https://en.wikipedia.org/wiki/Radioactive_decay]
Even though each atom is identical, the time required for decay varies among atoms, apparently randomly. What triggers the Weak Force to become active and the nucleus to emit energy and transform into other particles? Physicists cannot assign a cause to that. It is as though each atom chooses its own moment. (For more, see the entry Free Will Theorem.)

In contrast, in classical physics, nothing happens randomly. If a billiard ball rolls to the right, it’s because some force is pushing it in that direction. If we don’t know the nature of the force, it might seem like it’s random motion. But physicists tell us, rest assured, there is a prior causal force. The appearance of randomness is only a comment on our ignorance. This is to say that the mathematics of classical physics is deterministic—every physical action is determined by prior actions.
In the “true randomness” of quantum mechanics, we don’t know the cause and, also, many physicists say that there is none.
Quantum Randomness in Experimental Results
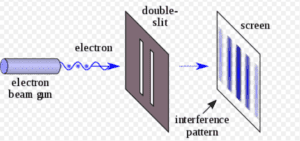
If the Double Slit Experiment is repeated numerous times, perhaps thousands of times, the results will reflect the probabilities of the Schrodinger Equation. For example, if the equation calculates a 50% probability for any particular position, 50% of electrons will be found to land in that position. However, physicists are unable to predict the position of any particular electron; the equation is silent on that question.
Quantum Randomness in Theory
Schrodinger’s Equation is a key equation of quantum mechanics. It, and the equations which were built upon it, have been extremely successful at predicting the behavior of quantum particles. Every day, physicists and engineers work with electronics on the assumption that quantum particles act, in certain ways, randomly but within the constraints of probability. Using the probabilistic equations of quantum mechanics, physicists have developed the modern electronics which have revolutionized our world: computers, cell phones, etc. So, physicists are confident of these equations. Yet, in many interpretations, the equations are not deterministic of individual particle behavior.
Could quantum particles be influenced by hidden variables?
The original interpretation of quantum mechanics, the Copenhagen Interpretation, assumes true randomness. While most later interpretations do as well, the Bohmian interpretation does not. David Bohm developed Bohmian Mechanics in the 1950’s. The equations of Bohmian Mechanics are the same as those of other forms of quantum mechanics except that Bohm added an additional equation.

Bohm’s interpretation holds that, just as in classical physics, randomness in quantum mechanics is apparent rather than real. Bohm built on the theories of Louis De Broglie. De Broglie hypothesized that an underlying force, a “pilot wave” was guiding the electron to its destination. In this view, the electrons are like surfers riding a wave. Bohm hypothesized that the pilot wave is an undetected force of nature. He described it with an equation that adds to the generally accepted equations of quantum mechanics.
It should be noted that Bohmian Mechanics is not entirely free of true randomness. It sneaks into the calculations as described in a series of videos on Bohmian Mechanics by “Looking Glass Universe” starting with this one.
So, is quantum randomness real or not?
Like so many other aspects of quantum mechanics, the jury is out regarding whether quantum randomness is real or whether quantum particles operate deterministically.
*The half-life of a radioactive material is the average time in which half of the atoms in the material will decay naturally. But the half-life cannot be used to calculate the moment that a particular atom will decay. Naturally occurring decay is spontaneous and cannot, at this time, be attributed to prior causes. However, shooting quantum particles at a nucleus (nuclear fission or fusion) can cause it to decay. This is not natural radioactivity.
