The Bohmian Interpretation is sometimes called the “Pilot Wave” or “Guiding Wave” Interpretation. It explains wave-particle duality by proposing that a real wave guides the quantum particle. For example, let’s consider


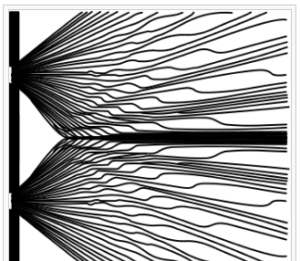
the Double Slit Experiment. In this experiment, an electron seems to act like a wave in that it can create an interference pattern much like a water wave would. The Bohmian Interpretation holds that a real wave creates the interference pattern. It guides the particle towards the detection screen, where the electron marks a dot. With repeated runs of the experiment, electrons make additional dots on the detection screen, eventually revealing the interference patterns created by the waves which have guided them.
This contrasts with the Copenhagen Interpretation. Many adherents of this interpretation maintain that the wave aspect of the particle is purely a mathematical expression (called a “wave function”). In this interpretation the mathematical expression has no physical meaning. And what’s more, it’s considered unscientific to ask questions about the physical meaning. This may seem odd, but it’s a notion based on the philosophy of Logical Positivism. Logical Positivism holds that science should concern itself only with that which can be measured. As the wave aspect of the particle cannot, in principle, be measured, it is a misunderstanding of science to ask about the reality or physical meaning of the wave function.
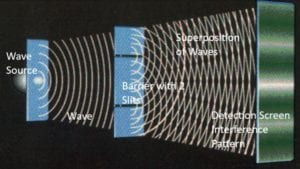
The guiding wave is not of the same order of reality as a physical wave such as a sound wave. A sound wave travels through a medium of air. The guiding wave travels through a field called the “quantum potential.” One of the peculiarities of the quantum potential wave is that it is described by wave functions (equations that describe waves) that generally include imaginary numbers—numbers that include the square root of negative one. We cannot assign physical reality to an imaginary number. What number when squared equals 1? There is none. The quantum potential field cannot, even in principle, be measured with scientific instruments.
The Copenhagen Interpretation similarly relies on a mathematical expression, the wave function, which generally includes imaginary numbers. However, in this interpretation, the wave function is nothing more than a way of calculating experimental results. It is not a description of reality. So, there is no need to address the physical meaning of imaginary numbers which appear in this mathematical expression.
Returning to the Bohmian Interpretation. In this interpretation, measurement does not cause wave function collapse and the formation of a particle. Instead, the quantum particle starts as a particle and continues as a particle. There’s always a particle and there’s always a wave. The particle always has definite properties even when not measured.
Bohmian Interpretation and Randomness
Whereas the Copenhagen Interpretation is not deterministic and includes the concept that a particle acts randomly, the Bohmian Interpretation is deterministic. In the Bohmian Interpretation, there is no true randomness only the appearance of randomness due to our ignorance.
In the Bohmian Interpretation, the appearance of randomness is explained as follows: The behavior of the particle can be fully explained by influences exerted on the guiding wave. The guiding wave, in turn, affects the particle which rides it. When the particle is measured, the guiding wave is disturbed, thus disturbing the particle. The particle lands on different positions on the detection screen because it starts in slightly different positions. The appearance of random behavior on the part of the particle is due only to our ignorance about the different initial positions of the particle and how the guiding wave is being influenced by forces. The particle is not manifesting true randomness; instead, its position (and other properties) is determined.
Why isn’t the Bohmian Interpretation more popular?
The Bohmian explanation so appeals to common sense that you might think it would be universally accepted as the most sensible interpretation of quantum mechanics. However, it has not been terribly popular among physicists. There are several reasons:
- Many physicists use the calculations of quantum mechanics without bothering about the physical reality that quantum mechanics describes. Quantum mechanics has been successfully used to develop computers and all the other electronic gadgets of our age. So physicists can accept the original interpretation of quantum mechanics, the Copenhagen Interpretation, without much concern about its descriptions of reality or whether these create any paradoxes. They are satisfied to follow the prescription that goes along with the Copenhagen Interpretation, “Shut up and calculate.” 1
- The Copenhagen Interpretation is considered to be simpler as the Bohmian Interpretation requires an additional equation. However, the downside of the Copenhagen’s simplicity is that it leaves unexplained mysteries, especially, the Measurement Problem.
- Some physicists are uncomfortable with ascribing reality to a new, undetectable field like the quantum potential.
- The Bohmian Interpretation is explicitly non-local. That is, it requires that all particles in the universe be interconnected and part of a single whole. Of course, non-locality due to particle entanglement has become widely accepted as an experimental phenomenon of quantum mechanics. The Copenhagen Interpretation provides no explanation for this phenomenon but scientists can hardly ignore the experimental support for it.
- Finally, the Bohmian Interpretation has some difficulty in applying its classical-type explanations when it comes to spin. This is described below in the section of “contextuality.”
The Bohmian Interpretation and Realism
The Bohmian Interpretation has the advantage of providing sensible (classical) explanations for experimental phenomena like wave function collapse and quantum entanglement. These remain paradoxes or riddles in the Copenhagen Interpretation. Copenhagen deals with these paradoxes by remaining silent about quantum behavior in between measurements. In fact, Copenhagen claims that discussion of the behavior of particles in between measurements is “unscientific.” In Niels Bohr’s2 understanding, Copenhagen grants no reality nor definite properties to particles when not measured. He maintained that there is no quantum realm. Thus, Copenhagen is open to Einstein’s charge that it rejects realism. Realism is the principle that an objective reality exists independent of observation of it and/or independent of our minds.
Einstein was a great believer in realism. He is quoted as saying, “I think that a particle must have a separate reality independent of the measurements. That is, an electron has spin, location and so forth even when it is not being measured. I like to think that the moon is there even if I am not looking at it.”
According to Bohm, “[A]ll particles have definite positions whether or not anyone is looking at them.”3 In other words, quantum particles are objectively real independent of our ability to observe them. At the same time, Bohm agreed with Bohr that we can never know the nature of those properties until they are measured. In the Bohmian Interpretation, the quantum realm is real but is hidden not only in practice but also in principle.
A Bohmian Exception to Realism? Contextuality
It should be noted that the Bohmian Interpretation seems to include an exception to realism when it comes to the measurement of spin and some other specific properties of particles. 4
To return to the Copenhagen Interpretation for a moment, particles such as electrons do not, in principle, have defined spin until measured. Measurement of spin is dependent upon the sequence in which the direction of spin is measured. Let’s say, for example, that the type of spin up/down vs. left/right is measured for a particular particle in this sequence:
- Up-down spin is measured, and the particle is found to have up-spin.
- Left-right spin is measured, and it might be found to have right spin.
But if the spin is measured in a different sequence, the results for the same particle might be:
- Left-right spin is measured, and it might be found to have left spin.
- Up-down spin is measured, and the particle is found to have down-spin.
In other words, the sequence in which the type of spin is measured can result in different outcomes. This would seem to rule out the possibility of realism. That is, the particles did not have a definite spin until measured. And this is the Copenhagen Interpretation.
The Bohmian Interpretation yields the same empirical prediction regarding the outcome of the measurement as does Copenhagen. However, the Bohmian explanation preserves realism. It holds that the electron had a definite spin prior to measurement, but spin can be changed by measurement. Measurement cannot tell us the pre-existing spin of the particle, since measurement can change the spin. Measurement is, after all, a form of interaction with another particle, and interactions can change the properties of a particle.
The Bohmian Interpretation is that a definite pre-existing property has been changed by measurement. This is called “contextuality.” Due to contextuality, the order in which spin is measured can change the spin of the particle. Contextuality does not affect measurements of position, momentum, or energy. However, it affects measurements of the polarization of light.
Does Bell’s Theorem rule out realism?
One final comment about the Bohmian Interpretation and realism—It might be thought that the successful experiments on Bell’s Theorem and entanglement rule out realism. This is not the case. Experiments (like those of Alain Aspect) which provide evidence of entanglement rule out local realism (or virtually rule it out). However, as noted below, the Bohmian Interpretation is not based on local realism. It is a non-local theory. The Bohmian Interpretation is compatible with the evidence provided by entanglement experiments and, actually, provides an explanation for entanglement. In part, it was Bohm’s work that inspired John Bell to explore entanglement and develop Bell’s Theorem.
The Bohmian Interpretation and Macroscopic Objects
The Bohmian Interpretation is a further development of the Guiding Wave Interpretation proposed by French physicist, Louis de Broglie. When de Broglie originally proposed the guiding wave idea at the famous 1927 Solvay Conference on quantum mechanics, objections were raised. One of those objecting was Hans Kramers, a Dutch physicist and student of Niels Bohr, co-founder of the Copenhagen Interpretation. Kramers pointed out that “[W]hen a photon bounces off a mirror, the mirror must recoil slightly from the impact. But de Broglie’s theory, according to Kramers, could not explain the mirror’s recoil. De Broglie admitted he could not answer this objection.”5
This objection was addressed by Bohm. He proposed that the mirror and other macroscopic objects should be considered as being composed of quantum particles. Of course, these days (2019) this is a widespread view among physicists. But at the time, the Copenhagen Interpretation held that macroscopic objects follow classical laws, and only quantum particles should be analysed in accordance with quantum laws. Bohm showed that if the mirror in Kramers’ example is seen as following the same quantum laws as the photon, the recoil of the mirror can be explained.
The Bohmian Interpretation and the Heisenberg Uncertainty Principle
In the Bohmian Interpretation, the Heisenberg Uncertainty Principle holds, just as it does in the Copenhagen Interpretation: The greater the certainty in the measurement of momentum, the less the certainty in the measurement of position. And vice versa. In addition, the Uncertainty Principle holds that neither property of a quantum particle can ever be measured exactly. According to the Copenhagen Interpretation, the fuzziness of the measurements is due to the lack of definition of the particles not due to difficulties we have in measuring. But according to the Bohmian Interpretation, the particles, themselves, have exactly defined properties at all times. As in Copenhagen, the problem is not with our measuring instruments. Instead, in the Bohmian Interpretation, it’s that Nature has effective mechanisms for hiding the exact properties from us.
Non-Locality
The Bohmian Interpretation is explicitly non-local. Einstein famously called this “spooky action at a distance.” Non-locality means that effects are created across distances at a speed faster than light and, perhaps, even instantaneously. The Bohmian Interpretation holds that all particles in the universe are entangled with each other. The behavior of one particle influences all other particles in the universe, regardless of distance. All particles in the universe share a single equation, a single wave function which is sometimes called the “universal wave function.” The entire universe evolves together in accordance with this giant equation.
Here is the Stanford Encyclopedia of Philosophy description of Bohmian non-locality. (It calls the Bohmian Interpretation by the sometimes used title, “Bohmian Mechanics.”) The quote also refers to the famous work of John Bell, who drew inspiration from Bohm’s interpretation.
“Bohmian mechanics makes explicit the most dramatic feature of quantum theory: quantum nonlocality….
“It should be emphasized that the nonlocality of Bohmian mechanics derives solely from the nonlocality… built into the structure of standard quantum theory. This nonlocality originates from a wave function on configuration space, an abstraction which, roughly speaking, combines—or binds—distant particles into a single irreducible reality. As Bell has stressed,
‘That the guiding wave, in the general case, propagates not in ordinary three-space but in a multidimensional-configuration space is the origin of the notorious ‘nonlocality’ of quantum mechanics. It is a merit of the de Broglie-Bohm version to bring this out so explicitly that it cannot be ignored.’ (Bell 1980, reprinted 1987c: 115)”6
Due to its explicit non-locality, the Bohmian Interpretation is able to explain the mechanism of entanglement in a way that the Copenhagen Interpretation cannot. Entanglement seems to require influences that travel faster than light. That would violate the speed limit for matter and energy assumed in Special Relativity. In contrast, the Bohmian Interpretation posits that two entangled particles act in a coordinated manner, regardless of distance, because they are part of the same thing.
This fits the mystics’ view that “we are all one.” But it doesn’t fit the view of many physicists. David Bohm was very engaged by the idea of holism, a concept important in Buddhism as well as other Eastern religions. It’s also important in New Age philosophies. His book Wholeness and the Implicate Order, as well as some of his other writings, explore the implications of quantum physics for issues of locality and holism.
History of the Bohmian Interpretation