« Back to Glossary Index

A wave is a movement that propagates through a medium. The accompanying animation demonstrates the motion of a seismic wave, the wave created by an earthquake, traveling through the Earth.

In a wave, a motion of one particle instigates the same motion in a neighboring particle. A wave that travels through the crowd in a football stadium is a good metaphor for a wave in physics. Each person or group stands and inspires their neighbor to stand. The motion ripples through the crowd.

The people aren’t moving their bodies down the bench–they each sit down again in exactly the same seat. But something is moving around the stadium—a motion—up and then down. The up/down/up motion is called an “oscillation.” Unlike in physics, the people aren’t physically making each other stand—it’s a mental connection. Each person has decided that when my neighbor stands and then starts to sit, I’ll stand up.

The stadium wave is a good metaphor for a physical wave. In a physical wave, a particular motion, an oscillation, is communicated from one bit to the next bit of some medium. Of course, a physical wave doesn’t involve a mental connection; it involves a physical push or pull on the neighboring particle. The neighboring particle then pushes or pulls on the next, and so on.

In brief, a wave is a transfer of motion through a medium. Motion is directed energy, so a wave is also a transfer of energy through a medium.

Water Waves as an Example

Repeating myself here—a wave, as defined in physics, is not the moving of an object from one place to another. When you’re standing on a river bank watching water rush downstream, you’re not watching a wave. You’re watching the water molecules, bits of matter, flowing in a direction. The water molecules are moving downstream. They are not staying in the same location and communicating motion to a neighboring molecule. They are not oscillating.

Of course, a river also includes actual waves in the physics sense, where water molecules are instigating motion in each other. So, rivers include both flows of water, where the molecules are moving downstream, and waves, where they are oscillating. The accompanying photo of a canoe being paddled downstream illustrates a flow of matter—the canoe and the water are flowing downstream. In addition, waves, where water molecules are oscillating, ruffle the surface of the water.

Another example of a mix of flows and waves is the surf rolling in. Yes, we call those tumbling, foaming things “waves.” But they don’t fit the physics definition of “waves.” The water molecules are rushing, let’s say, 30 feet up onto the sand. The molecules are moving from one place to another, not jiggling in place and communicating their motion to a neighbor. A physicist would say that the water crawling over the beach is not a wave in the physics sense because it’s not a transfer of motion or energy from one location to the next. To the contrary, it’s a motion of matter from one location to the next.

Waves out in the ocean, as opposed to those washing up onto the beach, are waves in the physics sense. These are called “deep ocean waves.” In a deep ocean wave, each bit of water moves up and down as well as sideways. They oscillate. It’s a more complex wave motion than the up/down/up wave that moves through the crowd in a stadium.

The accompanying animation shows that it’s actually a spiraling motion that travels from neighbor to neighbor. You can see this most easily if you follow the motion of one of the two red dots on the surface of the water. When we look at the surface of the ocean, we can’t see the spiraling oscillation. It’s a horizontal motion that is prominent.

Sound Waves as an Example

Sound is created by a different kind of wave. It’s a series of compressions and rarifications (thinning out) of air molecules. These compressions and rarifications push neighboring molecules so that they are physically influenced to repeat the same motions. This creates a propagating wave that travels rhythmically through the air. The accompanying video shows how sound waves work. The section in minutes 1:30 to 4:20 is most relevant, though the entire video is an excellent presentation on sound waves.

Electromagnetic Waves as an Example

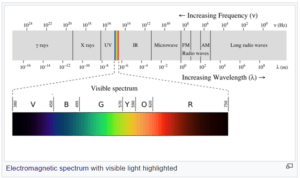
Electromagnetic waves include all the waves of the electromagnetic spectrum: X-rays, visible light, microwaves, radio waves, and others.

 

 

 

 

 

 

 

 

 

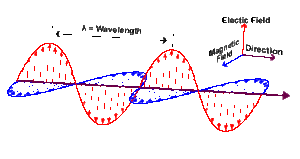
An electromagnetic wave is formed by an electric field giving rise to a magnetic field, which, in turn, gives rise to an electric field, and on and on. In other words, an electric field arises and smoothly expands perpendicular to the direction of travel. Then, it smoothly contracts in extent and disappears. A magnetic field then arises, smoothly expands, and, then, smoothly contracts and disappears. And on and on. The two fields are perpendicular to each other and to the line of travel.

What is the medium of an electromagnetic wave?

In the examples of the seismic wave, stadium wave, and water and sound waves, the mediums have been obvious. The seismic wave travels through the Earth; the stadium wave travels through people; the water wave travels through, well…water; and the sound wave travels through air. But what is the medium for an electromagnetic wave?

Until the 1900’s, scientists focused mostly on one kind of electromagnetic wave—visible light. And, until 1800, most scientists thought that light was a stream of particles rather than a wave. Once experimental evidence for the wave nature of light was accepted in the early 1800’s, scientists posited that it traveled through the “luminiferous ether.” This was thought of as an invisible medium that permeated all of space.

However, the luminiferous ether was never found. The study of electromagnetism in classical physics seems to have no problem with the missing medium. It shrugs its collective shoulders and moves on.

However, the question of the missing medium for electromagnetic waves is a central puzzle of quantum physics today. The issue takes the form of debate about the nature of the reality of quantum waves—are they simply mathematical objects, that is, concepts, or what? Many physicists, such as Nobel Laureate, Frank Wilczek, maintain that the medium is invisible quantum fields that fill “empty space.” Here, “empty space” means empty of matter but filled with quantum energy.

For more information on this issue, see the entry for quantum mechanics interpretations.

Waveforms

Waves take on a variety of shapes or “waveforms.” The accompanying image shows a plane wave—a wave that takes the shape of a plane. This image is a still from the animation of a seismic wave at the top of this article.

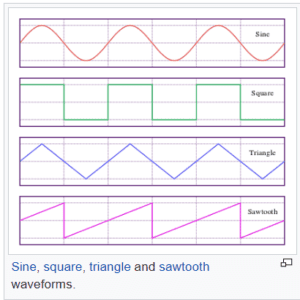
Electromagnetic waves (shown in section above) take on a shape called “sinusoidal” because they look like the graph of a trigonometric sine function.

Examples of a few waveforms, including a sinusoidal wave, appear in the accompanying diagram. There are many other waveforms.

Transverse vs. Longitudinal Waves

Waves are categorized as either transverse or longitudinal. A transverse wave experiences an oscillation which is perpendicular to the direction in which the wave travels.

The accompanying animation shows a transverse wave. The wave rises and falls, it oscillates up and down, while it travels horizontally to the right.

The metaphorical wave in the stadium is a transverse wave—the people are oscillating up and down but the wave ripples horizontally along the benches. The deep ocean wave is mostly a transverse wave—the water is oscillating up and down. However, a deep ocean wave also has a component of longitudinal motion. The overall effect is to create a kind of spiraling motion, as in the animation in the section above on water waves. In the ocean, we see the wave as traveling horizontally even though it is primarily experiencing an up and down oscillation.

Electromagnetic waves are also transverse. Their fields expand and contract perpendicularly to the line of travel.

What about sound waves? Sound waves are longitudinal. The motion of the individual molecules of air is parallel (not perpendicular) to the direction that the wave is traveling.

The accompanying animation shows a longitudinal wave. It may take a bit to see the difference between this motion and that in the animation of the transverse wave.

Notice that the longitudinal wave isn’t rising and falling. Instead the little rectangles are expanding and contracting horizontally as the wave ripples towards the right. The oscillation of expansion and contraction runs parallel to the horizontal direction that the wave is travelling.

Wave Properties vs. Particle Properties

At the macroscopic level of tables and chairs, the distinction between waves and particles is clear-cut. Waves are a form of energy moving through a material medium, that is, through matter. In contrast, particles are tiny bits of matter. But, at the quantum level, things get complicated.

The term “wave” has been applied at the quantum level on analogy to the term “wave” in the macroscopic world of tables and chairs. However, quantum waves have somewhat different properties from macroscopic waves such as water waves and sound waves. This is discussed in the next section.

In addition, at the quantum level, both energy and matter share in wave and particle properties. This is “wave-particle duality.” To appreciate wave-particle duality, it’s necessary to know the key differences between waves and particles. These are listed in the table below, followed by more detailed discussion.

Properties	Wave	Particle
Spread out or localized?	Spread out	Localized
Characterized by:
Frequency?	Yes	No
Wavelength?	Yes	No
Refraction?	Yes	No
Superposition/Diffraction/Interference?	Yes	No
Velocity calculated as:	For classical waves—Dependent on the medium For electromagnetic waves—frequency times wavelength	Velocity takes into account speed & direction
Momentum calculated as:	Proportional to wavelength	Mass times velocity
Energy calculated as:	For classical waves—Dependent on wave height For quantum waves—Dependent on frequency	E = mc2

Spread-out movement. A wave is a spread-out movement of energy through matter.

This is in contrast to a particle, which is localized in space. For example, a bullet can be thought of as a particle—at any moment in time, its position is in one small place.

Here is the animation of a seismic wave again—it’s spread out. A seismic wave radiates from an epicenter and declines in strength with distance. However, it may be measurable hundreds or even thousands of miles from the epicenter. In theory, if we had a sufficiently sensitive seismograph, we could detect a seismic wave anywhere on Earth.

Wave Frequency, Wavelength, and Speed

Wave motions occur in cycles. In the case of the metaphor of a wave running through a stadium, the cycle is: seated position—stand with hands in air—sit down again. That’s one complete cycle. The wave is created when the cycle is repeated over and over. Water waves, sound waves, and many other waves occur in cycles that are repeated to a beat; they have a rhythm. This gives waves a frequency, that is, a fixed number of cycles per unit of time. More specifically, frequency is the number of crests of the cycle (number of times someone stands up) per second.

In the accompanying image, the frequency is the number of crests that occur per second. Or one could say, it’s the number of troughs per second. If we were standing in one place and the wave were flowing by us, it would be the number of crests (or troughs) that we could count flowing past each second.

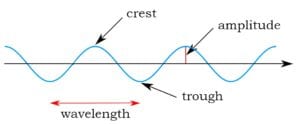
The period of a wave is the time between each crest. It is the time which one cycle takes to complete.

Waves also have a wavelength, that is, the physical distance covered in one cycle, from crest to crest or from trough to trough. In contrast, particles have neither frequency nor wavelength.

Frequency is not the same as the speed of travel of the wave. For an ordinary wave, for example, a sound wave traveling from the orchestra to the audience, the speed with which the sound reaches the audience depends upon the medium through which it travels. Let’s say that the sound is traveling through air, perhaps in San Francisco, at sea level on a pleasant May day. Then, the sound will reach the audience at about 770 miles per hour. If instead, the orchestra were performing in an unheated hall in Kathmandu in winter, the sound would travel slightly more slowly than 770 miles per hour. The colder the medium, the slower the speed of sound.

Electromagnetic waves, when traveling through a vacuum, like in outer space, always travel at the speed of light. That is 186,282 miles per second. For an electromagnetic wave, the frequency of the wave times its wavelength always equals the speed of light. This works out mathematically because wave frequency is inversely correlated with wavelength. The higher the frequency, the shorter the wavelength.   

Particles, like waves, have the property of speed. We can measure the speed of a bullet when shot from a gun, which travels as a particle, or the speed of light wave traveling from the Sun to Earth. However, physicists often focus on the velocity of a particle rather than its speed alone. Velocity includes both speed and direction of movement.

When speaking of waves, speed and velocity are the same thing. In contrast to the treatment of particles, direction is not lumped together with speed when computing the velocity of the wave.

Refraction is the bending of waves due to their traveling from one medium into another. The bent look of a spoon which is partly submerged in water is due to refraction.

 

When light waves travel through both air and water to arrive at our eyes, their bending results in the objects appearing to be in a different location from their actual location. The bending is due to the difference in speeds that light waves travel through air and through water. More specifically, it’s due to portions of the wave emerging from the water and into our eyes at different times from other portions of the wave.

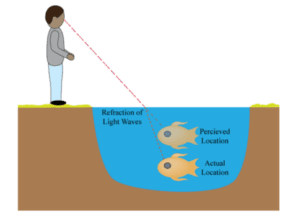
In the accompanying diagram, light waves travel from a single fish at the bottom of the pond, through the water, then the air, and finally, hit the eyes of the boy. The bending of the light when the light changes media from water to air is refraction. The result is that the fish appears to the boy to be higher in the water (the “perceived location”) than it actually is (the “actual location”).

In contrast, particles do not experience refraction. It’s true that particles may change velocity as they travel from one medium to another. For example, consider a bullet that shoots through the air and then, flies into a lake. When it hits the water, it might be slowed down and even experience a change in trajectory, but it does so as a single unit. Portions of it don’t experience different velocities—so, refraction doesn’t occur.

Superposition, Diffraction, and Interference            

Waves display three related behaviors that particles are not capable of: superposition, diffraction, and interference.

Superposition occurs when the effects of one wave add to the effects of another. One wave piggybacks on the other, creating what appears as a new wave that is the sum of the two, called a “superposition.”

The accompanying diagram of superposition shows two different situations. On the left, Wave 1 and Wave 2 are in phase, that is, their crests and troughs form at the same moment in time. If they were to flow together in the “Combined Wave,” they would reinforce each other, creating higher crests and deeper troughs. This increases their amplitude, the distance from the midline (shown in black) to the top of the crest (or—same measurement—the bottom of the trough).

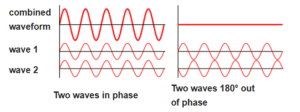
Here’s how a superposition could form. Let’s say a pebble were thrown into a pond. It would create circles of waves. Let’s say a second pebble were thrown in exactly the same spot and (miraculously) created exactly the same wave pattern—its waves were in phase with the waves of the first. Then, the combined waves would be double in height (amplitude) compared to the waves of the first pebble.

On the right side of the accompanying diagram is another possible outcome of throwing the second pebble. Its ripples might be (miraculously) precisely out-of-phase with the ripples of the first pebble. Then, the two sets of ripples would cancel each other. The resulting combined wave would not look like a wave at all. The water would appear flat.

Of course, in reality, the ripples of the second pebble would likely be neither perfectly in-phase nor perfectly out-of-phase with the ripples of the first. So, the most likely outcome would be partial cancellation—a combined wave with reduced crests and troughs relative to those of the first pebble.

Waves Resume After a Superposition. An interesting feature of waves is that they retain their integrity. Should two waves combine in a superposition and then separate, each would emerge and resume its original shape and properties as if nothing had happened. This is shown in the accompanying animation of a superposition.

In this animation, two waves approach each other, one from the right and one from the left. They meet in phase, that is, crest hits crest simultaneously. They move into a superposition, that is, they overlap each other. As they are in phase, their crests reinforce each other and create a new higher crest.

Then, the two waves continue traveling in opposite directions. They emerge out of superposition and resume their prior heights as if nothing had happened. The crests are back to what they were before the two waves went into superposition. (Of course, in real life, depending upon the type of wave and medium, there might be some loss of energy due to the superposition.)

What would happen if the waves were completely out-of-phase—the crest of one precisely hitting the trough of the other? The superposition would look completely flat, as if there were no wave present at all. Here’s what’s amazing—after the two waves emerged from this completely flat superposition, they would still resume their prior heights! What a remarkable aspect of wave behavior!

As a note, wave superposition can also be called “wave interference”—waves intercepting each other and either reinforcing each other or canceling each other.

Diffraction occurs when waves bend around obstructions. For example, light waves can travel through a slit in a barrier and, then, when “set free” on the other side, bend and fill the space. (See accompanying image to the left.) For example, sound waves can bend around corners of a building. Thus, we can hear sounds that come from around a corner. As another example, water waves can bend around a boat.

Diffraction Pattern. A diffraction pattern can form when waves from two or more sources interact. The accompanying image to the right is a drawing of the diffraction pattern formed when light shines through two slits in a barrier. The slits are on the extreme left. When light shines through them from the left, they form two sources of light waves. The resulting pattern is like the familiar crisscrossing ripples formed when two pebbles are thrown into a pond. The waves are in a superposition. Dark areas form where the waves cancel each other; light areas form where the waves reinforce each other.

Not all superpositions of waves form diffraction patterns. The waves must have similar frequencies and amplitudes among other requirements.

“Interference pattern” is another name for a diffraction pattern. Waves are said to interfere with each other when they form a superposition in which the waves largely cancel each other (destructive interference) or reinforce each other (constructive interference).

Classical Waves and Quantum Waves Compared 

When scientists say that light can be thought of as traveling in waves, they are using the term “waves” to mean quantum waves. Quantum waves are called “waves” on analogy to waves in the macroscopic world, such as water waves and sound waves.

Light waves and waves of water, for example, have strong similarities. They both are spread out relative to particles. They both have frequencies and wavelengths. And there are other similarities as well. But in some ways, and notably the way in which they deliver energy, the analogy doesn’t hold.

The table below summarizes the similarities and differences of classical and quantum waves. For the most part, this article has addressed classical waves. For more information on quantum waves, see the entry on quantum waves.

Comparison of Classical Waves and Quantum Waves
Properties	Classical Wave	Quantum Wave
Is spread out?	Yes	Yes
Energy is quantized or continuous?	Continuous	Quantized
Has frequency, wavelength, & amplitude?	Yes	Yes
Refracts?	Yes	Yes
Interference is due to?	Waves of similar frequency & medium	Under debate—possibly with self
Speed of wave travel depends on?	Medium through which wave travels	Frequency times wavelength (applies to electromagnetic waves)
Energy depends on?	Amplitude	Frequency
Amplitude determines what?	Energy of wave	Probability of an associated particle being detected
Has a known medium?	Yes	Under debate—possibly quantum fields
Instruments have observed?	Yes	Under debate—possibly publicly verifiable by experimental results
Can be described solely with real numbers?	Yes	Real numbers plus imaginary numbers required

Footnotes