« Back to Glossary Index

This article is about superpositions of waves as understood In classical physics. See superposition, quantum mechanics for the later, quantum mechanical use of the term.

Superpositions of Waves That Are Perfectly in Sync (in Phase)

In classical physics, waves are said to be in a superposition when they meet and run through each other. The two waves are on top of each other, are in a “superposition,” and can interact in a number of ways. But upon parting, they return to their original characteristics.

In the accompanying video, two waves approach each other from opposite directions. These might be, for example, waves in water or sound waves in the air. Upon meeting, they amplify their heights—the heights of the two waves add together to make a taller wave. I find the next bit quite magical: once they’ve passed each other, they emerge unscathed as if nothing had happened. They return to their original heights. (To run the video in slow motion, perhaps at .5 speed, click on the Settings icon (a gear or cogwheel), then click Speed, then .25 (quarter-speed) or .5 (half-speed).)

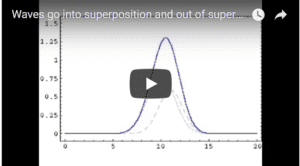
In this video the waves are perfectly in sync (technically “in phase”). That is, both waves go up into crests and go down into troughs at exactly the same moment. As noted, in this situation, they amplify each other before parting ways. The waves are said to create “constructive interference.” 

Superposition of Waves That Are Perfectly Out of Sync (Out of Phase) 

But, of course, waves might meet that are out of sync. That is, they might crest at different times. If they were perfectly out of phase so that one crested exactly at the moment that the other bottomed out, they would cancel each other. Upon meeting, it would appear that there were no waves at all. The water would go flat. Or, in the case of sound waves, the air would stop vibrating, creating no sound at all. These waves are said to create “destructive interference.” 

This is the principle behind White Noise. White Noise creates sound waves that cancel the sound waves that we don’t want to hear. The interacting sound waves go quiet. But, the waves haven’t really disappeared. Upon emerging from their superposition, the waves continue on, back to their old selves, as if nothing had happened.

Superposition of Other Waves

Often, waves meet which are neither perfectly in phase nor perfectly out of phase. In this situation, the two waves become amplified in some places and flattened out in others. The result is a superposition that looks like the accompanying drawing. The waves form the familiar crisscross ripples of two stones thrown into a pond or two boat wakes meeting. The crisscross pattern is created by crests created and troughs created by constructive interference as well as flat areas due to destructive interference.

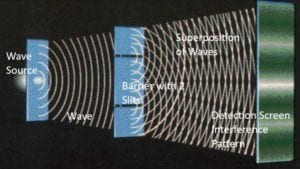
If the crisscross pattern should hit a vertical surface like a detection screen, the resulting pattern on the screen is striped with fringes. This is called an “interference pattern” or “diffraction pattern.”